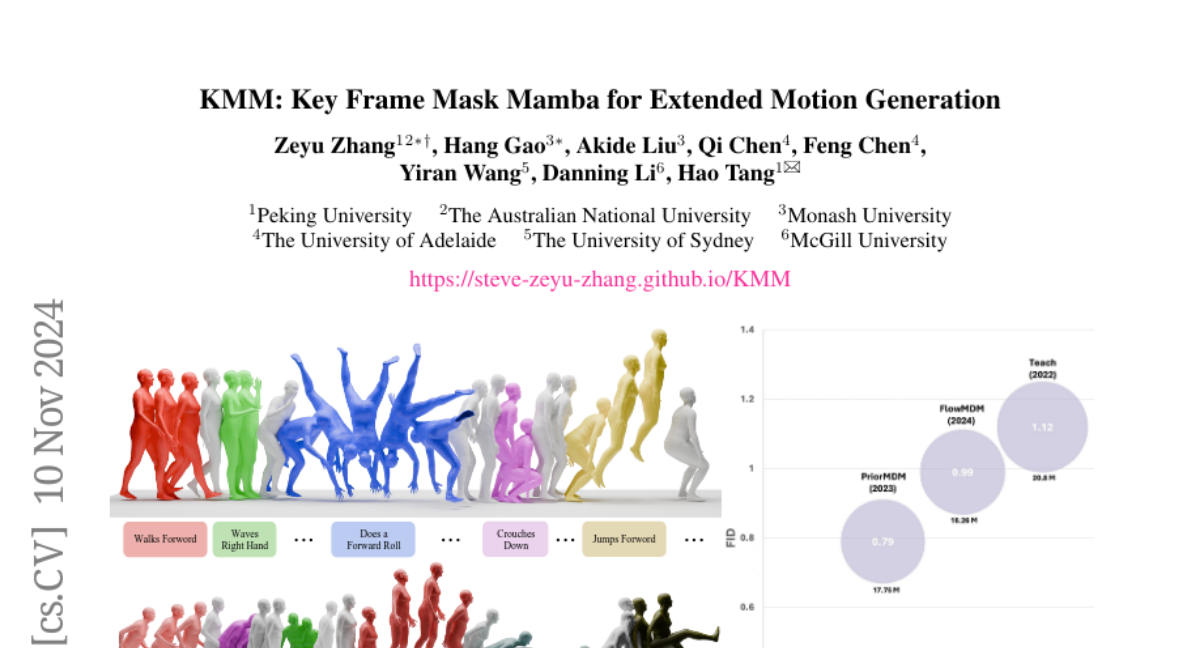
Ключевые кадры и маскирование Mamba для расширенного генерирования движений
Генерирование движений человека является одной из наиболее перспективных областей исследований в области генеративного компьютерного зрения. Эта технология находит применение в создании видео, разработке игр и манипуляциях роботами. Недавно разработанная архитектура Mamba показала многообещающие результаты в моделировании длинных и сложных последовательностей, однако остаются два значительных вызова:
- Прямое применение Mamba к расширенному генерированию движений неэффективно из-за ограниченной емкости неявной памяти, что приводит к затуханию памяти.
- Mamba испытывает трудности с мультимодальной интеграцией по сравнению с трансформерами и плохо согласуется с текстовыми запросами, часто путая направления (лево или право) или пропуская части длинных текстовых запросов.
В этой статье мы представляем три ключевых вклада для решения этих проблем:
- KMM (Keyframe Mask Modeling) - новая архитектура, разработанная для улучшения фокуса Mamba на ключевых действиях в сегментах движения.
- Контрастивное обучение для улучшения мультимодальной интеграции и согласования текста с движением.
- Эксперименты на датасете BABEL, где наш метод достиг рекордных результатов, сократив FID на более чем 57% и количество параметров на 70% по сравнению с предыдущими методами.
Мотивация
Расширенное генерирование движений сталкивается с двумя основными проблемами:
- Генерация длинных последовательностей движений без ухудшения качества последних частей последовательности.
- Баланс между производительностью и эффективностью при обработке длинных последовательностей.
Архитектура Mamba, благодаря своей способности к рекурсивному моделированию и линейному масштабированию с длиной последовательности, является многообещающей для решения этих задач. Однако, прямое применение Mamba к расширенному генерированию движений сталкивается с проблемами:
- Ограниченная емкость неявной памяти, что приводит к затуханию памяти при генерации длинных последовательностей.
- Слабая мультимодальная интеграция из-за последовательной архитектуры, что ухудшает согласование между текстом и движением.
Методология
Ключевое кадровое маскирование
Мы разработали новый подход к выбору и маскированию ключевых кадров, основанный на плотности. Этот метод позволяет модели сосредоточиться на обучении с замаскированных ключевых кадров, что более эффективно для архитектуры неявной памяти Mamba, чем случайное маскирование.
Расчет локальной плотности
Пусть (X \in \mathbb{R}^{n \times l}) обозначает вложение движения в латентное пространство, где (n) - количество токенов во временной размерности, а (l) - пространственная размерность. Мы вычисляем матрицу парных евклидовых расстояний (D \in \mathbb{R}^{n \times n}):
[D_{i,j} = ||x_i - x_j||2 = \sqrt{\sum{k=1}^l (x_{i,k} - x_{j,k})^2}]
где (x_i) и (x_j) - это (i)-й и (j)-й ряды матрицы (X), а (x_{i,k}) и (x_{j,k}) - (k)-й элемент этих рядов.
Затем локальная плотность (d \in \mathbb{R}^n) вычисляется как:
[d_i = \sum_j \exp(-D^2_{i,j})]
Это представляет собой сумму значений гауссовых ядер, центрированных на каждом латентном векторе (x_i), где ширина ядра определяется квадратом расстояния (D^2_{i,j}).
Минимальное расстояние до более высокой плотности
Мы расширяем локальную плотность (d) в две промежуточные матрицы (d_{col} \in \mathbb{R}^{1 \times n}) и (d_{row} \in \mathbb{R}^{n \times 1}) для вещания, гарантируя, что каждый столбец и строка являются дубликатами локальной плотности (d). Затем создается булевская маска (M \in {0, 1}^{n \times n}):
[M_{i,j} = \begin{cases} 1, & \text{если } d_{col,i} < d_{row,j} \ 0, & \text{иначе} \end{cases}]
Эта маска используется для нахождения минимального расстояния до более высокой плотности:
[D_{masked} = D \odot M + (1 - M) \odot \infty]
где (\odot) обозначает поэлементное умножение.
Согласование текста и движения
Согласование текста и движения остается значительным вызовом, поскольку генеративные модели плохо понимают текстовые признаки, встроенные CLIP-кодером. Мы предлагаем использовать контрастивное обучение для уменьшения расстояния между текстовым и движением латентными пространствами.
Контрастивное обучение
Пусть (T_i) будут текстовыми латентами для (i)-го образца, и (M_j) - движением латентами для (j)-го образца. Сходство между текстовыми латентами (T_i) и движением латентами (M_j) вычисляется как:
[\text{sim}_{ij} = \frac{T_i^\top M_j}{\tau}]
где (\tau) - температурный параметр. Контрастивные метки определяются как (y = [0, 1, 2, ..., b-1]), и контрастивная функция потерь для текстовых и движением вложений выражается как:
[L_{\text{contrast}} = \frac{1}{2} \left( \text{CrossEntropy}(\text{sim}, y) + \text{CrossEntropy}(\text{sim}^\top, y) \right)]
Эксперименты
Датасеты и метрики оценки
BABEL Dataset - это стандартный бенчмарк для длинного генерирования движений, содержащий 10,881 последовательностей движений с 65,926 сегментами, каждый из которых связан с конкретным текстовым аннотациям.
BABEL-D Dataset - подмножество тестового набора BABEL, включающее направленные условия с ключевыми словами, такими как "лево" и "право", что делает его более сложным для оценки.
Сравнительные исследования
Наш метод KMM был обучен и оценен на датасете BABEL, показав значительное превосходство над предыдущими подходами к генерированию движений по длинным последовательностям. Результаты показаны в таблицах 1 и 2.
Таблица 1: Сравнение на датасете BABEL
| Модели | R-precision ↑ | FID ↓ | Diversity → | MM-Dist ↓ | |----------------------|---------------|---------|-------------|-----------| | Ground Truth | 0.715 ± 0.003 | 0.00 | 8.42 ± 0.15 | 3.36 | | TEACH | 0.460 ± 0.000 | 1.12 | 8.28 | 7.14 | | ... | ... | ... | ... | ... | | KMM (Ours) | 0.666 ± 0.001 | 0.34 ± 0.01 | 8.67 ± 0.14 | 3.11 ± 0.01 |
Таблица 2: Сравнение на бенчмарке BABEL-D
| Модели | R-precision ↑ | FID ↓ | Diversity → | MM-Dist ↓ | |----------------------|---------------|---------|-------------|-----------| | Ground Truth | 0.438 ± 0.000 | 0.02 | 8.46 | 3.71 | | PriorMDM | 0.334 ± 0.015 | 6.82 | 7.27 | 7.44 | | KMM w/o Alignment | 0.484 ± 0.007 | 5.50 | 8.44 | 3.48 | | KMM (Ours) | 0.538 ± 0.009 | 3.86 ± 0.14 | 8.04 ± 0.14 | 2.72 ± 0.03 |
Заключение
В заключение, наше исследование решает две значительные проблемы в расширенном генерировании движений: затухание памяти при генерации длинных последовательностей и слабое согласование текста с движением. Наш метод KMM предлагает инновационные решения, значительно продвигая эту область вперед.