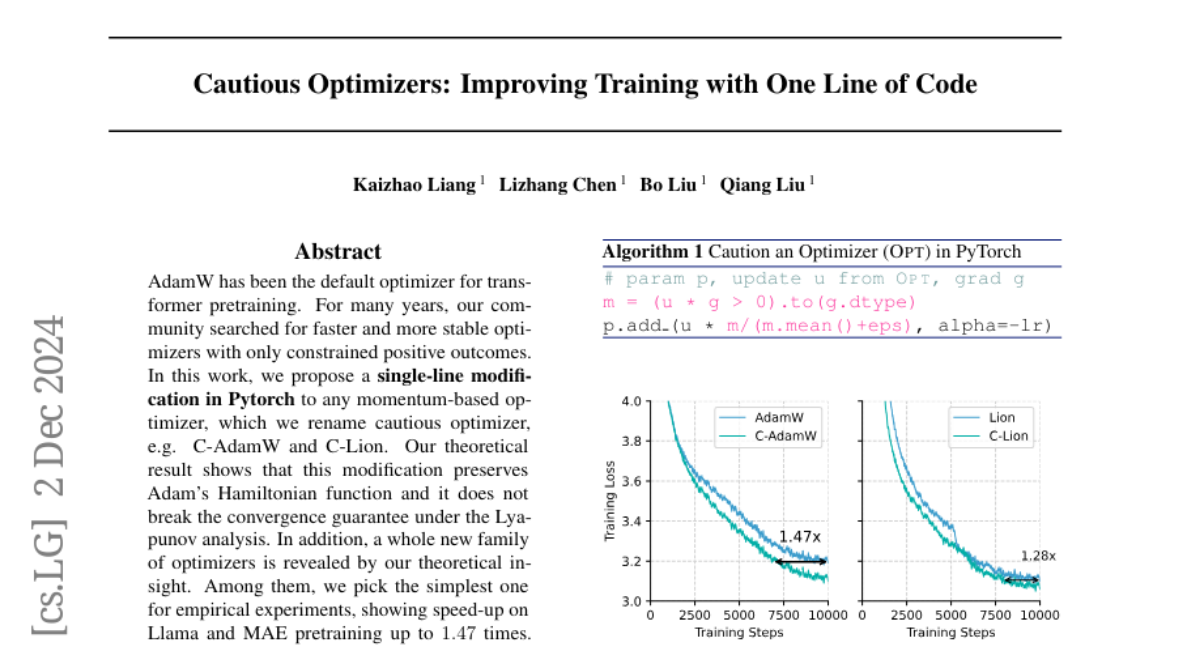
Осторожные оптимизаторы: Улучшение обучения одной строкой кода

В современном машинном обучении оптимизация играет ключевую роль, и поиск более быстрых и стабильных оптимизаторов остается актуальной задачей. В последние годы AdamW стал стандартным оптимизатором для предобучения трансформеров. Однако, несмотря на его эффективность, сообщество постоянно ищет способы улучшения. В данной статье мы представим новую концепцию, названную "Осторожные оптимизаторы" (Cautious Optimizers), которая предлагает простое, но эффективное улучшение любого оптимизатора на основе импульса (momentum-based) всего одной строкой кода.

С момента своего появления в 2014 году, оптимизаторы Adam и AdamW зарекомендовали себя как ключевые инструменты для обучения нейронных сетей. Однако, несмотря на их популярность, исследователи постоянно работают над созданием более эффективных альтернатив. В эпоху масштабирования моделей, где скорость обучения напрямую влияет на возможности модели, поиск оптимизаторов, превосходящих AdamW, становится особенно важным.

Недавние разработки, такие как LION, SHAMPOO, SOAP, ADOPT и Schedule-Free, обещают значительные улучшения по сравнению с AdamW. Однако эти методы либо требуют значительных вычислительных ресурсов, либо сложны в настройке гиперпараметров, что ограничивает их широкое применение. В свете этого, мы предлагаем "Осторожные оптимизаторы", которые представляют собой простое улучшение, требующее минимальных изменений в коде.

Основная идея

Осторожные оптимизаторы вносят небольшое, но мощное изменение в стандартные алгоритмы оптимизации. Суть изменения заключается в том, чтобы не обновлять параметры модели, если направление предлагаемого обновления не совпадает с текущим градиентом. Это достигается путем применения маски, которая обнуляет обновления, где направление градиента и предлагаемое обновление не согласованы.

Теоретические основы

Мы обозначим общее обновление оптимизатора следующим образом:

[ w_{t+1} \leftarrow w_t - \epsilon_t u_t ]

где ( w_t ) - параметры модели на шаге ( t ), ( u_t ) - направление обновления, а ( \epsilon_t ) - размер шага. В оптимизаторах на основе импульса ( u_t ) не всегда совпадает с градиентом ( g_t = \nabla L(w_t) ), что может привести к временному увеличению функции потерь и замедлению сходимости.

Осторожные оптимизаторы добавляют маску, основанную на согласованности знаков ( u_t ) и ( g_t ):

[ w_{t+1} \leftarrow w_t - \epsilon_t u_t \circ \varphi(u_t \circ g_t) ]

где ( \circ ) обозначает поэлементное умножение, а ( \varphi ) - функция, которая перераспределяет обновление на основе продукта ( u_t \circ g_t ). Мы выбираем ( \varphi(x) = I(x > 0) ), так что обновление обнуляется для координат, где знаки ( u_t ) и ( g_t ) не совпадают.

Преимущества

Это изменение гарантирует, что новое обновление имеет неотрицательное внутреннее произведение с градиентом, что монотонно уменьшает функцию потерь при достаточно малом размере шага. Теоретически, мы показываем, что модифицированный алгоритм сходится к локальным оптимумам при мягких условиях, наложенных на базовые оптимизаторы.

Практическое применение

Мы реализовали осторожные версии AdamW и Lion, обозначив их как C-AdamW и C-Lion соответственно. Эмпирические эксперименты показали, что эти версии достигают ускорения до 1.47x и 1.28x на предобучении моделей Llama и MAE на ImageNet1K без значительных накладных расходов.

Алгоритм C-AdamW

def C_AdamW(params, lr, betas=(0.9, 0.999), eps=1e-8, weight_decay=0):
    t, m, v = 0, 0, 0
    for param in params:
        if param.grad is None:
            continue
        g = param.grad
        t += 1
        m = betas[0] * m + (1 - betas[0]) * g
        v = betas[1] * v + (1 - betas[1]) * g ** 2
        m_hat = m / (1 - betas[0] ** t)
        v_hat = v / (1 - betas[1] ** t)
        u = m_hat / (v_hat.sqrt() + eps)
        phi = (u * g > 0).to(g.dtype)
        lr_t = lr * phi.sum() / (phi.sum() + 1)
        param.data.add_(-lr_t * u * phi)
        if weight_decay != 0:
            param.data.add_(-lr_t * weight_decay * param.data)

Алгоритм C-Lion

def C_Lion(params, lr, beta1=0.9, beta2=0.999, weight_decay=0):
    t, m = 0, 0
    for param in params:
        if param.grad is None:
            continue
        g = param.grad
        t += 1
        u = torch.sign(beta1 * m + (1 - beta1) * g)
        m = beta2 * m + (1 - beta2) * g
        phi = (u * g > 0).to(g.dtype)
        lr_t = lr * phi.sum() / (phi.sum() + 1)
        param.data.add_(-lr_t * u * phi)
        if weight_decay != 0:
            param.data.add_(-lr_t * weight_decay * param.data)

Заключение

Осторожные оптимизаторы представляют собой простой и эффективный способ улучшения существующих оптимизаторов на основе импульса. Они не только сохраняют гарантии сходимости базовых алгоритмов, но и ускоряют процесс минимизации функции потерь. В будущем мы планируем исследовать различные функции ( \varphi ), применение маскирования в пространстве собственных векторов, а также более строгий анализ для невыпуклых случаев.